Vertical Eddy Diffusivity in the Tropical Cyclone Boundary Layer during Landfall
Abstract
:1. Introduction
2. Material and Methods
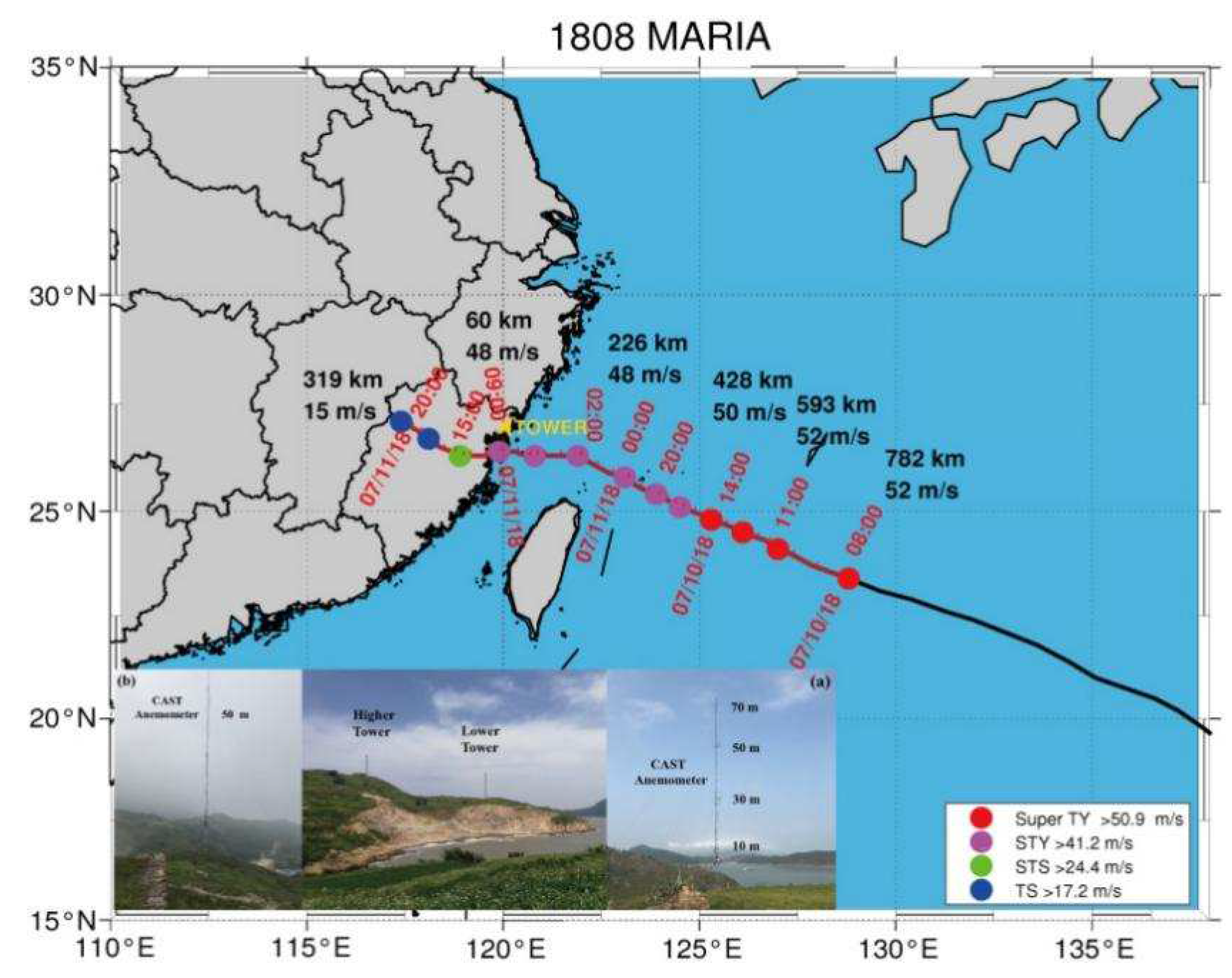
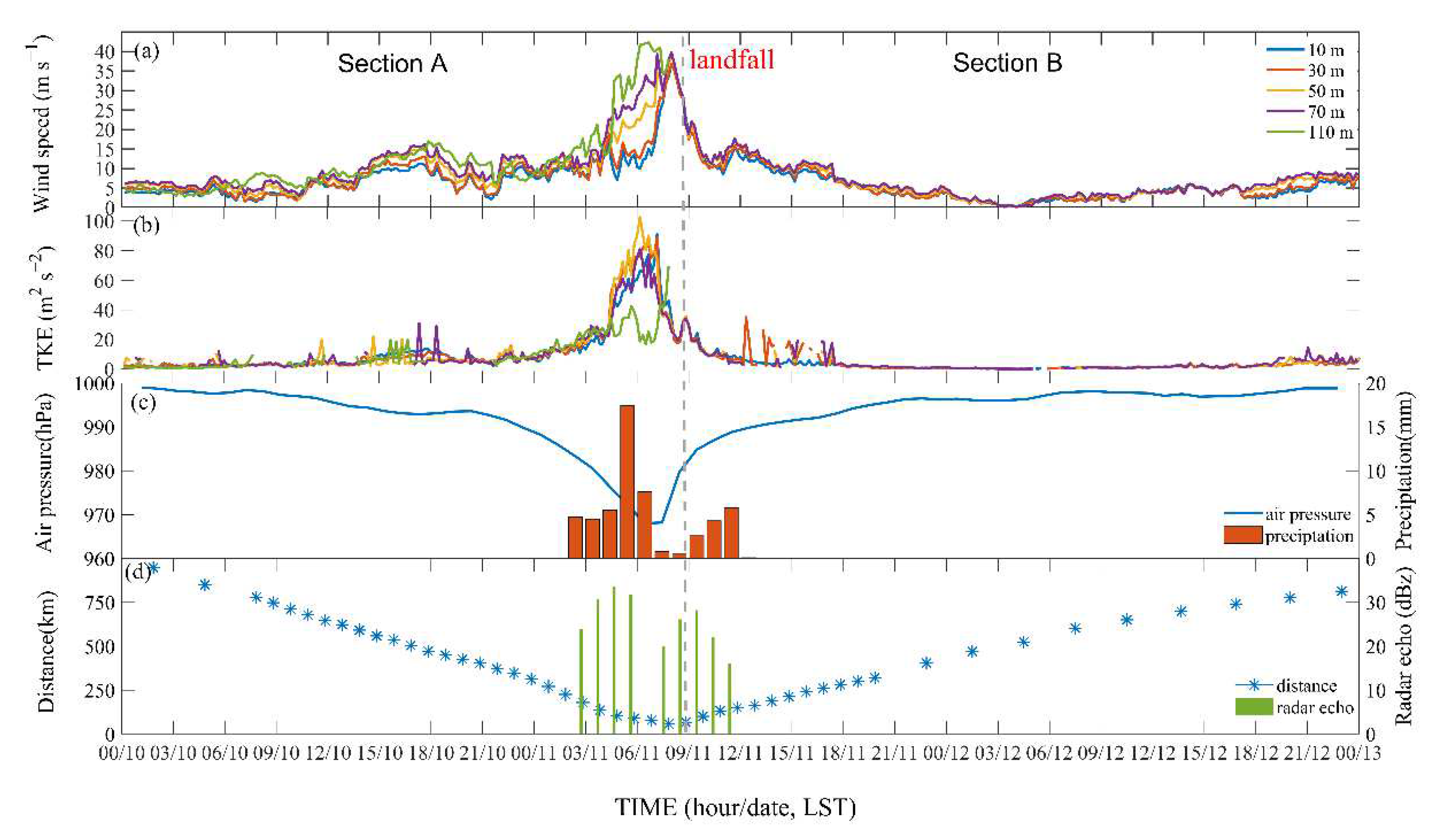
2.1. Review of Typhoon Maria
2.2. Observational Data and Analysis Method
2.2.1. Eddy Covariance Method
2.2.2. Data Processing and Quality Control
- (1)
- Spikes in the datasets were removed using the criterion X(h) < (X − 4) or X(h) > (X + 4), where X(h) denotes the original data, X is the mean over the averaging interval, and is the standard deviation [34].
- (2)
- The calculation of VED was omitted when the corresponding u* was < 0.01 m s−1. No gap filling was used.
- (3)
- Based on the coastline features near the measurement site, the onshore wind direction varied from 52.5° to 227.5°, and the offshore wind direction varied from 272.5° to 5°. The wind data from the back of the three-dimensional sonic anemometer measurements of the lower tower (249–269°) and higher tower (68–88°) were removed due to the turbulent eddies generated by the towers.
- (4)
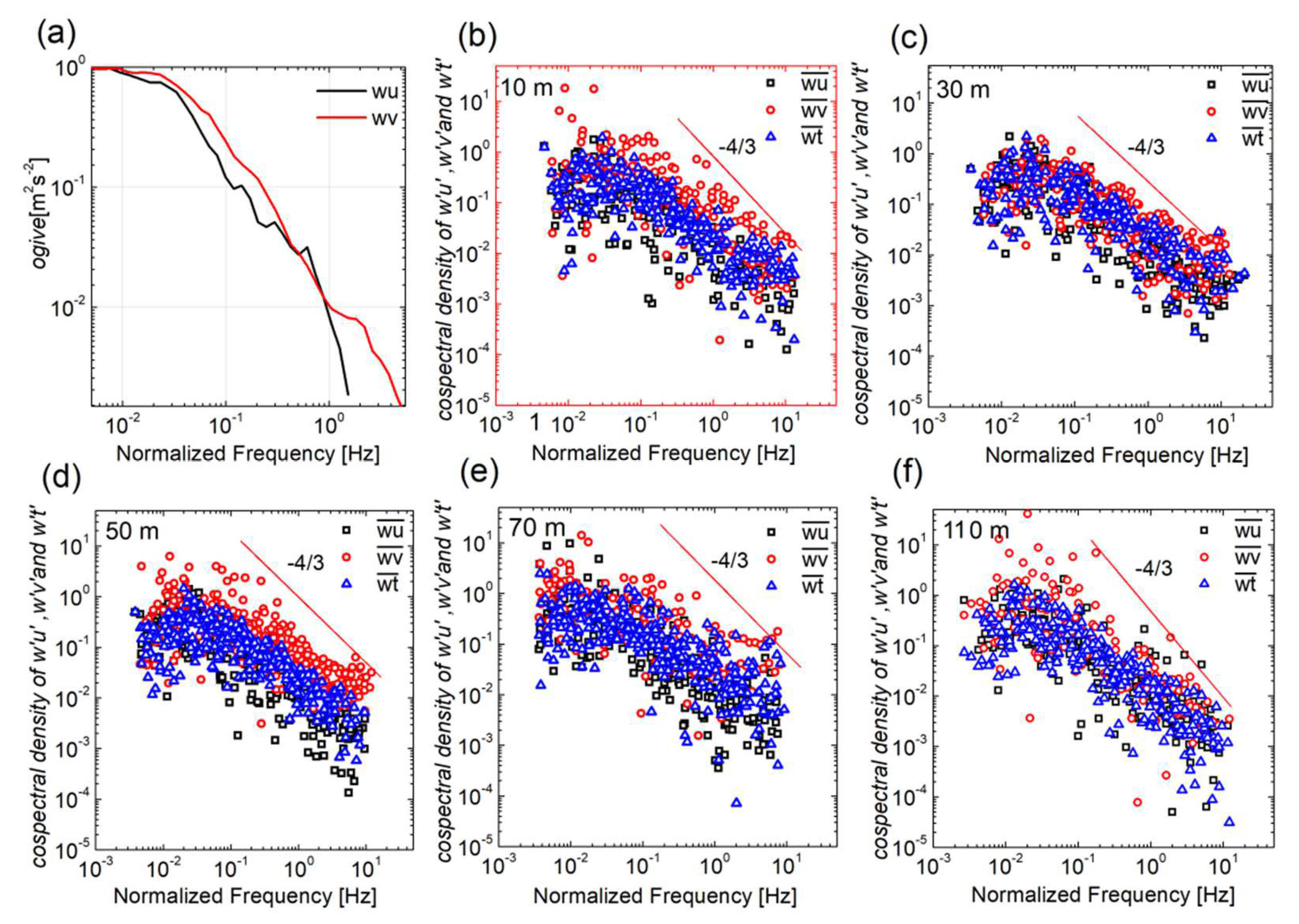
- Averaging period: A cumulative frequency curve (ogive) can be used to understand the turbulent stationarity and its spatial scale, which is then typically used to determine the appropriate time period required to calculate the turbulent flux [34].where x (= u, v, and T) denotes the along-wind (u) and cross-wind (v) components, and ultrasonic virtual temperature (T), respectively, is the cospectrum of w’u’, w’v’, and w’T’ at frequency . As we can see, for the ogive curves of w′u′, w′v′, and w′T′ shown in Figure 2a, the ogive curves of the w′u′, w′v′, and w′T′ approached a constant value at an averaging period of 5 min when it converged towards 0.005 Hz. Therefore, an averaging period more than 5 min is suitable for calculating the turbulent flux and can represent the total flux. Hence, we chose 10 min for the averaging period to calculate the moment and heat flux.
- (5)
- A turbulence (co)spectrum check.
3. Results and Discussion
3.1. General Meteorological Conditions
3.1.1. Wind Characteristics during the Observation Period
3.1.2. Meteorological Conditions
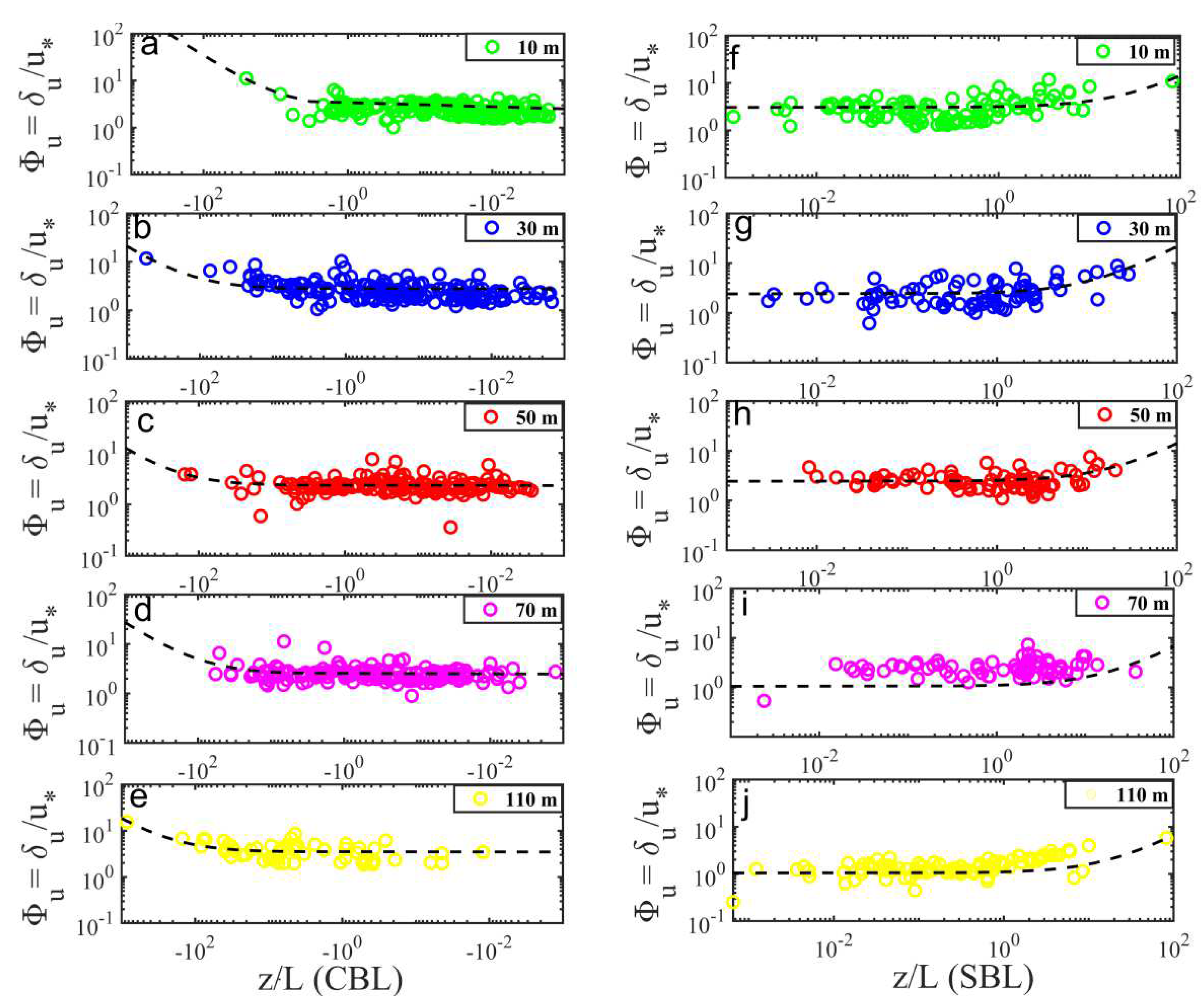
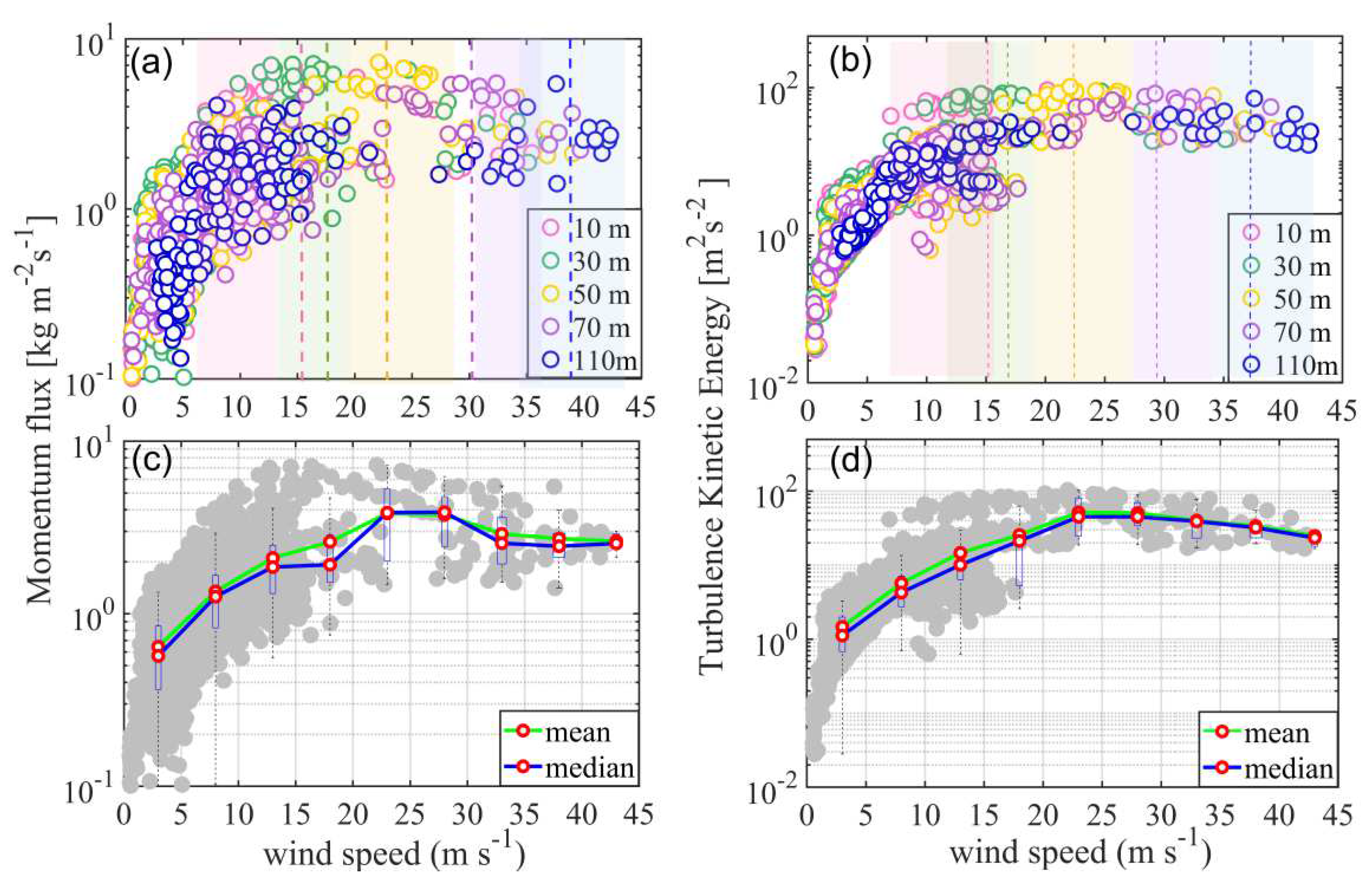
3.2. Variations in Momentum Fluxes and Turbulent Kinetic Energy with wind Speed at Each Height
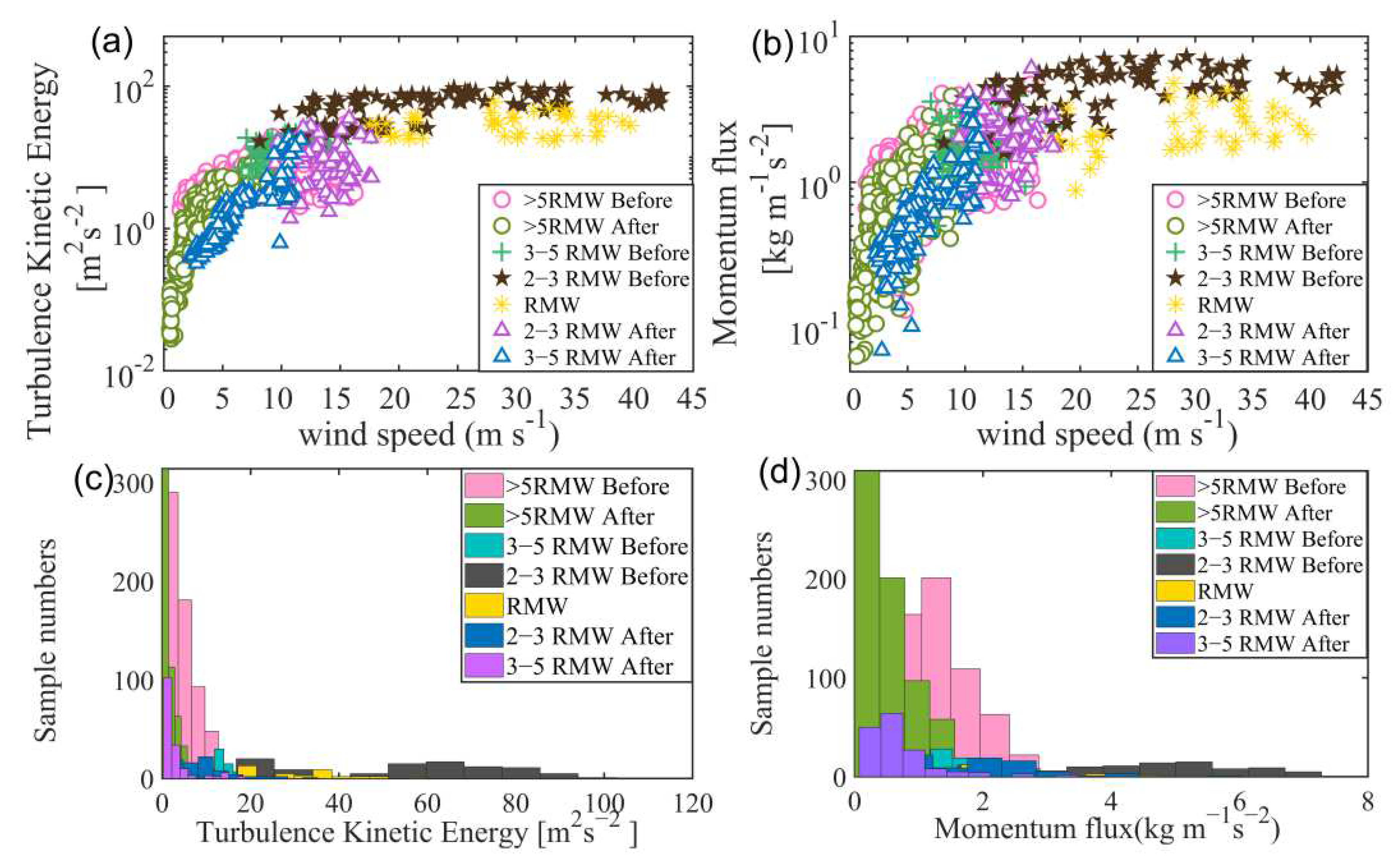
3.3. Variations in Momentum Fluxes and Turbulent Kinetic Energy with Distance from TC Center
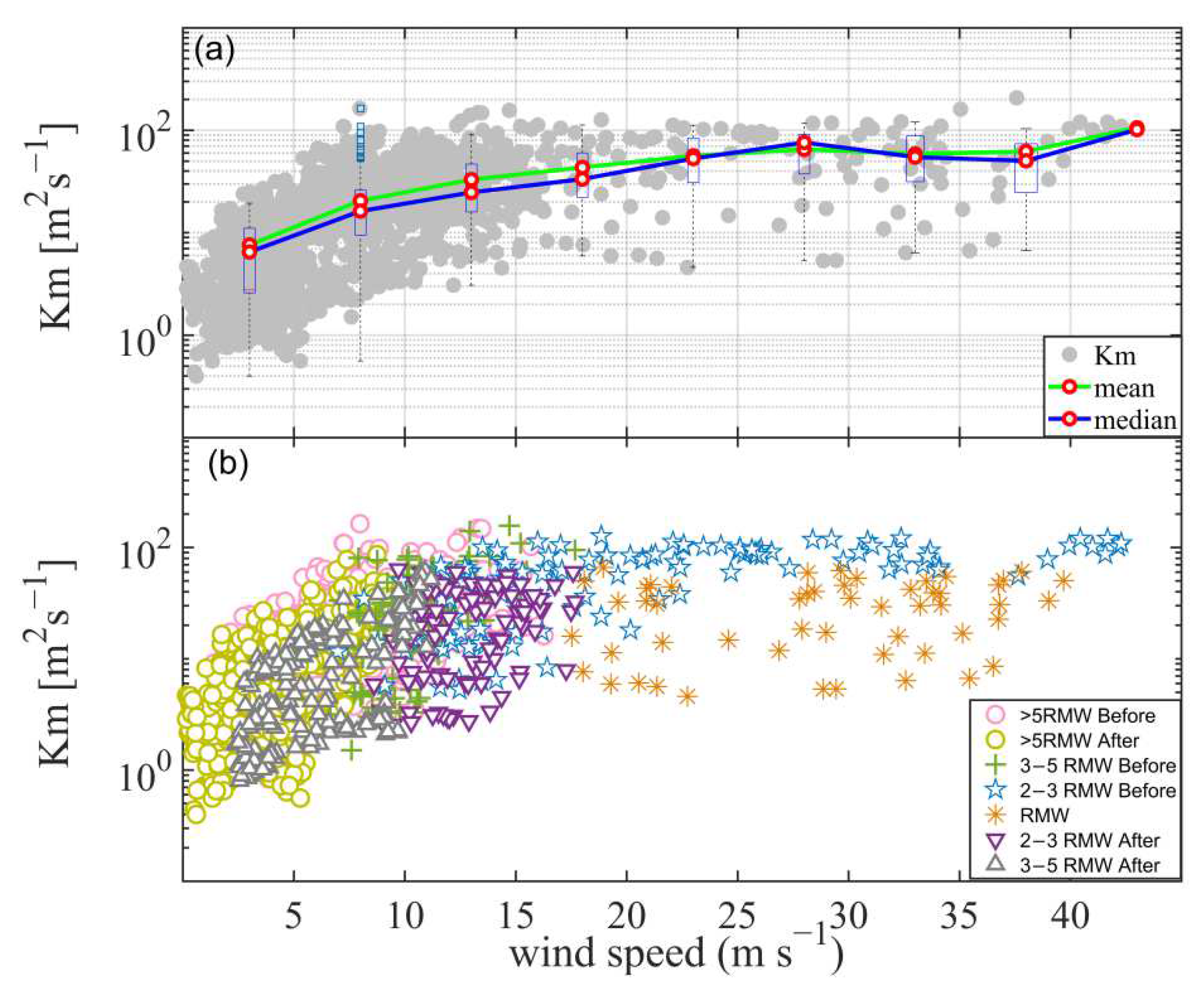
3.4. Vertical Diffusion Transport of Momentum
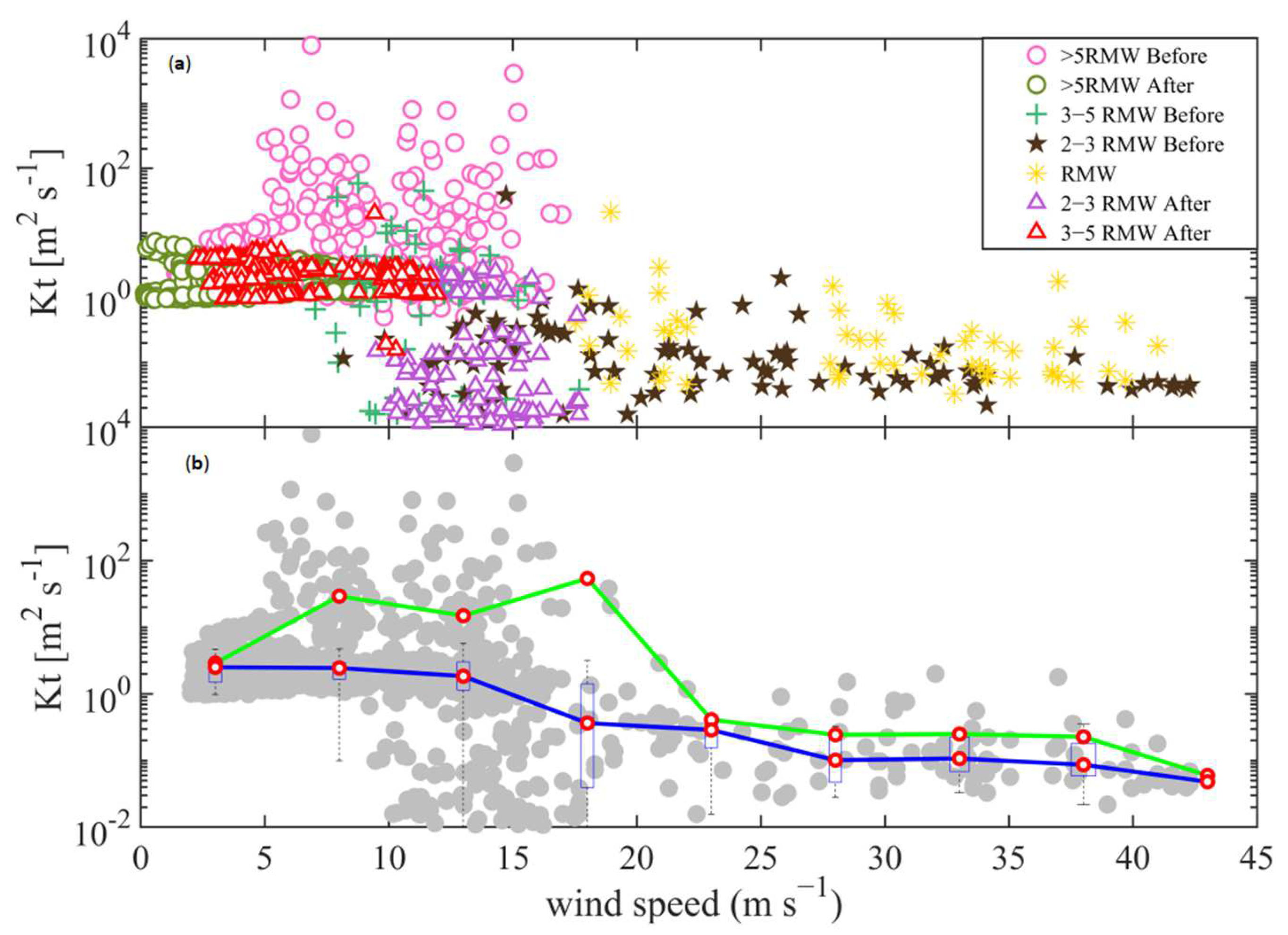
3.5. Vertical Eddy Diffusivity of the Sensible Heat Flux
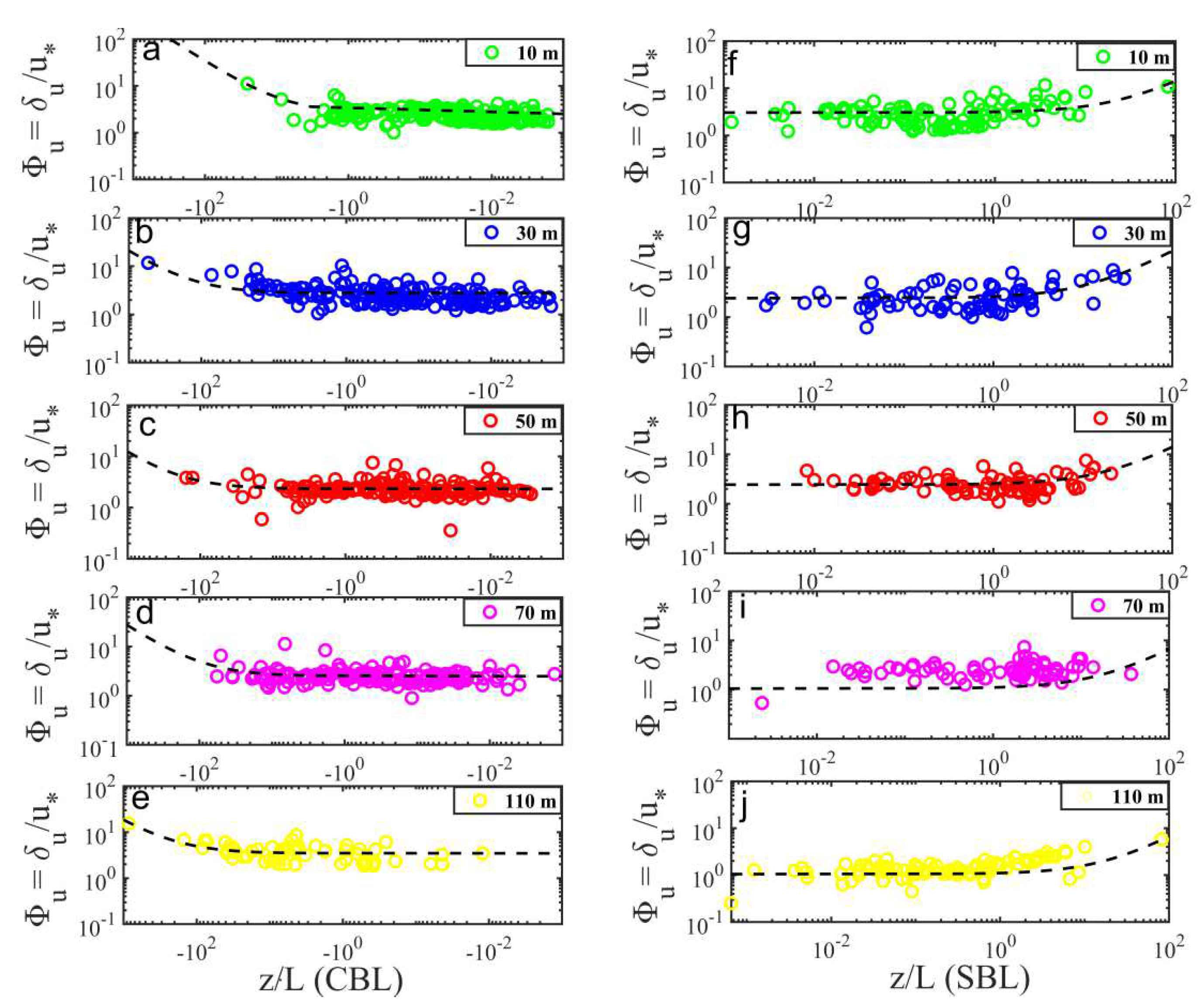
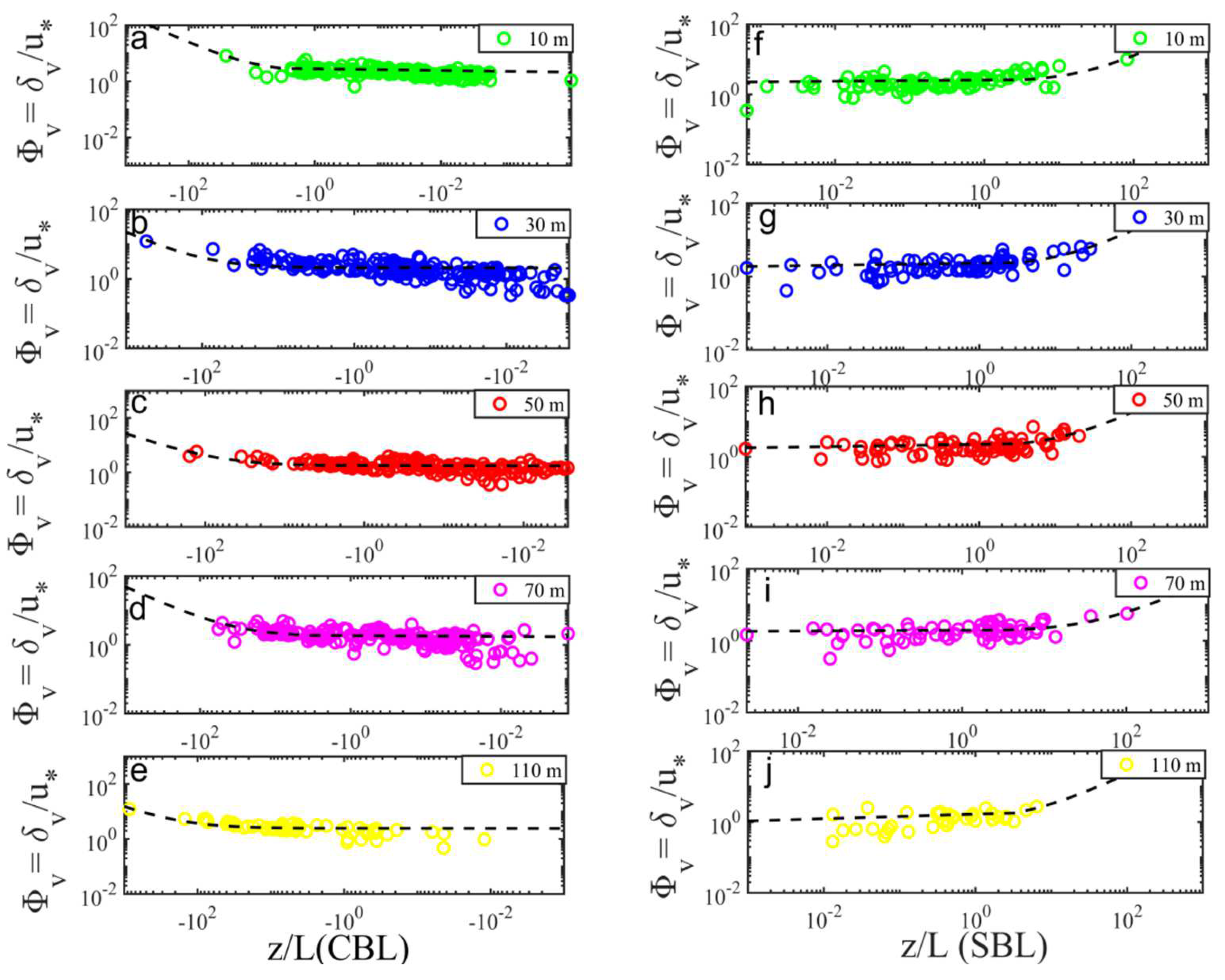
3.6. Variation in Vertical Mixing Length
3.7. Variations in the Strain Ratio
4. Conclusions and Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Emanuel, K.A. An air–sea interaction theory for tropical cyclones. Part I: Steady-state maintenance. J. Atmos. Sci. 1986, 43, 585–604. [Google Scholar] [CrossRef]
- Smith, R.K.; Montgomery, M.T.; Sang, N.V. Tropical cyclone spin-up revisited. Q. J. R. Meteorol. Soc. 2009, 135, 1321–1335. [Google Scholar] [CrossRef] [Green Version]
- Gopalakrishnan, S.G.; Marks, F.; Zhang, J.A.; Zhang, X.; Bao, J.-W.; Tallapragada, V. A study of the impacts of vertical diffusion on the structure and intensity of tropical cyclones using the high resolution HWRF system. J. Atmos. Sci. 2013, 70, 524–541. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.G.; Koch, D.; Upadhayay, S.; DeMaria, M.; Marks, F.; Rappaport, E.N.; Mehra, A.; Tallapragada, V.; Jung, Y.; Alaka, Jr.; et al. 2019 HFIP R&D Activities Summary: Recent Results and Operational Implementation; HFIP Technical Report: HFIP 2018–1.2020; National Oceanic and Atmospheric Administration United States Department of Commerce: Washington, DC, USA, 2019. Available online: http://www.hfip.org/documents/HFIP_AnnualReport_FY2019.pdf (accessed on 13 May 2022).
- Zhang, J.A.; Drennan, W.M. An observational study of vertical eddy diffusivity in the hurricane boundary layer. J. Atmos. Sci. 2012, 69, 3223–3236. [Google Scholar] [CrossRef]
- Zhu, P. Simulation and parameterization of the turbulent transport in the hurricane boundary layer by large eddies. J. Geophys. Res. 2008, 113, D17104. [Google Scholar] [CrossRef]
- Bao, J.-W.; Gopalakrishnan, S.G.; Michelson, S.A.; Marks, F.D.; Montgomery, M.T., Jr. Impact of physics representations in the HWRFX on simulated hurricane structure and pressure–wind relationships. Mon. Wea. Rev. 2012, 140, 3278–3299. [Google Scholar] [CrossRef] [Green Version]
- Kepert, J.D. Choosing a boundary layer parameterization for tropical cyclone modeling. Mon. Wea. Rev. 2012, 140, 1427–1445. [Google Scholar] [CrossRef] [Green Version]
- Zhu, P.; Menelaou, K.; Zhu, Z. Impact of sub-grid scale vertical turbulent mixing on eyewall asymmetric structures and mesovortices of hurricanes. Q. J. R. Meteorol. Soc. 2013, 140, 416–438. [Google Scholar] [CrossRef]
- Zhang, J.A.; Nolan, D.S.; Rogers, R.F.; Tallapragada, V. Evaluating the impact of improvements in the boundary layer parameterizations on hurricane intensity and structure forecasts in HWRF. Mon. Wea. Rev. 2015, 143, 3136–3155. [Google Scholar] [CrossRef]
- Zhang, J.A.; Zhu, P. Effects of vertical eddy diffusivity parameterization on the evolution of landfalling hurricanes. J. Atmos. Sci. 2017, 74, 1879–1905. [Google Scholar] [CrossRef]
- Ming, J.; Zhang, J.A.; Rogers, R.F. Typhoon kinematic and thermodynamic boundary layer structure from dropsonde composites. J. Geophys. Res. Atmos. 2015, 120, 3158–3172. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rogers, R.F.; Tallapragada, V. Impact of parameterized boundary layer structure on tropical cyclone rapid intensification forecasts in HWRF. Mon. Wea. Rev. 2017, 145, 1413–1426. [Google Scholar] [CrossRef]
- Li, X.; Pu, Z. Vertical eddy diffusivity parameterization based on a large-eddy simulation and its impact on prediction of hurricane landfall. Geophys. Res. Lett. 2020, 48, e2020GL090703. [Google Scholar] [CrossRef]
- Zhu, P.; Hazelton, A.; Zhang, Z.; Marks, F.D.; Tallapragada, V. The role of eyewall turbulent transport in the pathway to intensification of tropical cyclones. J. Geophys. Res. Atmos. 2021, 126, e2021JD034983. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, P.; Gao, Z.; Cheung, K.K. Sensitivity of large eddy simulations of tropical cyclone to sub-grid scale mixing parameterization. Atoms. Res. 2022, 265, 105922. [Google Scholar] [CrossRef]
- Nolan, D.S.; Zhang, J.A.; Stern, D.P. Evaluation of planetary boundary layer parameterizations in tropical cyclones by comparison of in-situ data and high resolution simulations of Hurricane Isabel (2003). Part I: Initialization, maximum winds, and outer core boundary layer structure. Mon. Wea. Rev. 2009, 137, 3651–3674. [Google Scholar] [CrossRef]
- Kepert, J.D. The dynamics of boundary layer jets within the tropical cyclone core. Part I: Linear theory. J. Atmos. Sci. 2001, 58, 2469–2484. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.A.; Marks, F.D.; Montgomery, M.T.; Lorsolo, S. An estimation of turbulent characteristics in the low-level region of intense Hurricanes Allen (1980) and Hugo (1989). Mon. Wea. Rev. 2011, 139, 1447–1462. [Google Scholar] [CrossRef] [Green Version]
- Gopalakrishnan, S.; Hazelton, A.; Zhang, J.A. Improving hurricane boundary layer parameterization scheme based on observations. Earth Space Sci. 2021, 8, e2020EA001422. [Google Scholar] [CrossRef]
- Black, P.G.; Asaro, E.A.D.; Sanford, T.B.; Drennan, W.M.; Zhang, J.A.; French, J.R.; Nüler, P.P.; Terrill, E.J.; Walsh, E.J. Air–sea exchange in hurricanes: Synthesis of observations from the Coupled Boundary Layer Air–Sea Transfer experiment. B. Meteorol. Soc. 2007, 88, 357–374. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.K.; Chan, P.W.; Wu, N.; Zhang, J.A.; Hon, K.K. Aircraft observations of turbulence characteristics in the tropical cyclone boundary layer. Bound. Layer Meteorol. 2020, 174, 493–511. [Google Scholar] [CrossRef]
- Katz, J.; Zhu, P. Evaluation of surface layer flux parameterizations using in-situ observations. Atmos. Res. 2017, 194, 150–163. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, J.A.; Aberson, S.D.; Marks, F.D.; Lei, X. Multilevel tower observations of vertical eddy diffusivity and mixing length in the tropical cyclone boundary layer during landfalls. J. Atmos. Sci. 2018, 75, 3159–3168. [Google Scholar] [CrossRef]
- Zhao, Z.; Gao, R.; Zhang, J.A.; Zhu, Y.; Liu, C.; Chan, P.W.; Wan, Q. Observations of Boundary Layer Wind and Turbulence of a Landfalling Tropical Cyclone. 20 August 2021, PREPRINT (Version 1) available at Research Square. Available online: https://www.researchgate.net/publication/354043506_Observations_of_Boundary_Layer_Wind_and_Turbulence_of_a_Landfalling_Tropical_Cyclone (accessed on 28 May 2022).
- Li, L.; Xiao, Y.; Zhou, H.; Xing, F.; Song, L. Turbulent wind characteristics in typhoon Hagupit based on field measurements. Int. J. Distrib. Sens. Netw. 2018, 14. [Google Scholar] [CrossRef]
- Xia, D.; Dai, L.; Lin, L.; Wang, H.; Hu, H. A Field Measurement based Wind Characteristics Analysis of a Typhoon in Near-ground Boundary Layer. Atmosphere 2021, 12, 873. [Google Scholar] [CrossRef]
- Lee, X.; Massman, W.; Law, B. Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis; Kluwer Academic Publishers: New York, NY, USA, 2004; pp. 33–66. [Google Scholar]
- Qin, Z.; Xia, D.; Dai, L.; Zheng, Q.; Lin, L. Investigations on wind characteristics for typhoon and monsoon wind speeds based on both stationary and non-stationary models. Atmosphere 2022, 13, 178. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean Tech. 2014, 31, 287–301. [Google Scholar] [CrossRef] [Green Version]
- Bao, X.; Wu, L.; Zhang, S.; Li, Q.; Lin, L.; Zhao, B.; Wu, D.; Xia, W.; Xu, B. Distinct raindrop size distributions of convective inner- and outer-rainband rain in Typhoon Maria (2018). J. Geophys. Res. Atmos. 2020, 125, e2020JD032482. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; p. 670. [Google Scholar]
- Schmid, H.P.; Grimmond, C.S.B.; Cropley, F.; Offerle, B.; Su, H.B. Measurements of CO2 and energy fluxes over a mixed hardwood forest in the mid-western United States. Agric. Forest Meteorol. 2000, 103, 357–374. [Google Scholar] [CrossRef]
- Foken, T.; Göockede; Mauder, M.; Mahrt, L.; Amiro, B.; Munger, W. Handbook of Micrometeorology: Post-Field Data Quality Control; Lee, X., Massman, W., Law, B., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 181–208. [Google Scholar]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Akad. Nauk. SSSR. Geofiz. Inst. Trudy 1954, 151, 163–187. [Google Scholar]
- Fortuniak, K.; Pawlak, W. Selected Spectral Characteristics of Turbulence over an Urbanized Area in the Centre of Łód’z, Poland. Bound. Layer Meteorol. 2015, 154, 137–156. [Google Scholar] [CrossRef] [Green Version]
- Kaimal, J.C.; Wyngaard, J.C.; Coté, O.R. Spectral characteristics of surface-layer turbulence. Q.J.R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Ortiz-Suslow, D.G.; Kalogiros, J.; Yamaguchi, R.; Wang, Q. An evaluation of the constant flux layer in the atmospheric flow above the wavy air-sea interface. J. Geophys. Res. Atmos. 2021, 126, e2020JD032834. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structures and Measurements; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Grachev, A.A.; Leo, L.S.; Fernando, H.J.S.; Fairall, C.W.; Creegan, E.; Blomquist, B.W.; Christman, A.J.; Hocut, C.M. Air-sea/land interaction in the coast. Bound. Layer Meteorol. 2018, 167, 181–210. [Google Scholar] [CrossRef]
- Grachev, A.A.; Krishnamurthy, R.; Fernando, H.J.S.; Fairall, C.W.; Bardoel, S.L.; Wang, S. Atmospheric turbulence measurements at a coastal zone with and without Fog. Bound. Layer Meteorol. 2021, 181, 395–422. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rogers, R.F. Effects of parameterized boundary layer structure on hurricane rapid intensification in shear. Mon. Wea. Rev. 2019, 147, 853–871. [Google Scholar] [CrossRef]
- Lükö, G.; Torma, P.; Weidinger, T. Intra-Seasonal and Intra-Annual Variation of the Latent Heat Flux Transfer Coefficient for a Freshwater Lake. Atmosphere 2022, 13, 352. [Google Scholar] [CrossRef]
- Dudorova, N.V.; Belan, B.D. The Energy Model of Urban Heat Island. Atmosphere 2022, 13, 457. [Google Scholar] [CrossRef]
- Yang, L.; Qian, F.; Song, D.-X.; Zheng, K.-J. Research on Urban Heat-Island Effect. Procedia Eng. 2016, 169, 11–18. [Google Scholar] [CrossRef]
- Kalina, E.A.; Biswas, M.K.; Zhang, J.A.; Newman, K.M. Sensitivity of an Idealized Tropical Cyclone to the Configuration of the Global Forecast System–Eddy Diffusivity Mass Flux Planetary Boundary Layer Scheme. Atmosphere 2021, 12, 284. [Google Scholar] [CrossRef]
- Do Nascimento, A.C.L.; Galvani, E.; Gobo, J.P.A.; Wollmann, C.A. Comparison between Air Temperature and Land Surface Temperature for the City of São Paulo, Brazil. Atmosphere 2022, 13, 491. [Google Scholar] [CrossRef]
- Elmarakby, E.; Khalifa, M.; Elshater, A.; Afifi, S. Tailored methods for mapping urban heat islands in Greater Cairo Region. Ain Shams Eng. J. 2021. [Google Scholar] [CrossRef]
- Li, J.; Collins, R.; Lu, X.; Williams, B. Lidar observations of instability and estimates of vertical eddy diffusivity induced by gravity wave breaking in the Arctic mesosphere. J. Geophys. Res. Atmos. 2021, 126, e2020JD033450. [Google Scholar] [CrossRef]
- Shi, W.; Tang, J.; Chen, Y.; Chen, N.; Liu, Q.; Liu, T. Study of the Boundary Layer Structure of a Landfalling Typhoon Based on the Observation from Multiple Ground-Based Doppler Wind Lidars. Remote Sens. 2021, 13, 4810. [Google Scholar] [CrossRef]




| First Peak | Second Peak | |||
|---|---|---|---|---|
| Onshore (52.5–227.5°) | Offshore (272–5°) | |||
| Instrument Height (m) | Wind Speed (m s−1) | Wind Direction (°) | Wind Speed (m s−1) | Wind Direction (°) |
| 10 | 16.57 | 300.22 | 36.51 | 48.28 |
| 30 | 19.05 | 316.41 | 36.79 | 51.17 |
| 50 | 22.26 | 234.08 | 39.06 | 47.72 |
| 70 | 29.61 | 243.53 | 39.67 | 42.17 |
| 110 | 21.28 | 329.92 | 42.27 | 54.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C. Vertical Eddy Diffusivity in the Tropical Cyclone Boundary Layer during Landfall. Atmosphere 2022, 13, 982. https://doi.org/10.3390/atmos13060982
Chen C. Vertical Eddy Diffusivity in the Tropical Cyclone Boundary Layer during Landfall. Atmosphere. 2022; 13(6):982. https://doi.org/10.3390/atmos13060982
Chicago/Turabian StyleChen, Chen. 2022. "Vertical Eddy Diffusivity in the Tropical Cyclone Boundary Layer during Landfall" Atmosphere 13, no. 6: 982. https://doi.org/10.3390/atmos13060982
APA StyleChen, C. (2022). Vertical Eddy Diffusivity in the Tropical Cyclone Boundary Layer during Landfall. Atmosphere, 13(6), 982. https://doi.org/10.3390/atmos13060982





